Discriminant Validity through Fronell-Larcker Criterion

Last updated on Apr 26, 2020 2 min read Discriminant Validity, Exploratory Factor Analysis

Before reading this post, we assume the reader has at least a basic understanding of discriminant validity as explained here.

The Fronell-Larcker criterion is one of the most popular techniques used to check the discriminant validity of measurements models. According to this criterion, the square root of the average variance extracted by a construct must be greater than the correlation between the construct and any other construct. Once this condition is satisfied, discriminant validity is established.

Below are the steps necessary for establishing the Fronell-Larcker criterion.

  1. Compute the Average for each construct as demonstrated here

  2. Find the correlation among the construct (you must use the average you computed for each construct in step 1 above).

Don’t know how to find correlation in SPSS, check here.

The SPSS output is shown below.

Table 1

Table 1 presents you with Pearson Correlation, level of significance of this correlation (Sig. 2 tailed) and the sample size (N). We are interested in the Pearson correlation together with the asterisk (*) indicating the significance level.

Table 2

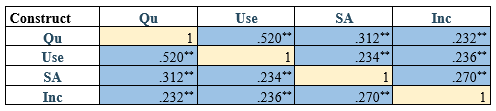
So, we create a new table (see Table 2) and input these items. Note that for correlations, the items on the upper diagonals are the same as those on the lower diagonals (see Table 2). Hence, we delete the upper diagonals (see Table 3).

Table 3

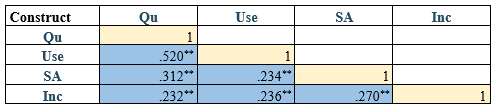
Nice! But we are not done yet.

Next, we replace the ones (“1“) on the diagonal with the square roots of its AVE (see our post on AVE for the digits ).

For example, the correlation between SAT and SAT is 1 .i.e. corr(Qu,Qu) = 1, so we replace the 1 with $\sqrt{\text{(AVE for Qu)} = \sqrt{0.658} = 0.811$

Similarly, for Use, $\sqrt{(\text{AVE for Use})} = \sqrt{0.648} = 0.805$ etc.

So, you need to do these for all the constructs and record your values.

Table 4

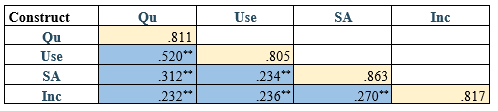
Once this is done, you need to check and make sure the correlation of a construct with other constructs are less than the square root of its AVE.

For example,

  1. corr(Use,Qu) = 0.520 < 0.805 (True)

  2. corr(SA,Qu) = 0.312 < 0.863 and corr(SA,Use) = 0.234 < 0.863 (True)

….

After a careful check, you will notice this criterion is satisfied. Once this is done, you have successfully established the discriminant validity of your study.

If this criterion is not met, then there is a problem with your questionnaire, thus, the items you claim are UNrelated are in fact related.

Did you find this page helpful? Consider sharing it 🙌

Discriminant Validity Exploratory Factor Analysis
Next
Previous

Related